Evaluation of the relationship between Monson's sphere and arch form and cusp angle using three-dimensional reconstruction method

서 론

교합만곡에는 시상면에서의 전후방만곡인 스피만곡 (Spee, 1890)과 전두면에서의 측방만곡인 윌슨만곡 (Wilson, 1911)이 있다. 몬슨은 이 두 교합만곡을 합하면 반지름 101.60 mm (4 inch)의 구를 이룬다는 ‘몬슨의 4 inch 구면설 (Monson's 4 inch spherical theory)’을 제창하였다 (Monson, 1920). 몬슨 구는 임상적으로 치아의 결손, 정출 및 경사 등에 의해서 생긴 치열 부정의 보철이나 구강재건술을 시행할 때 교합만곡의 결정기준으로서 널리 응용되고 있다 (Bonwill, 1885; 최아영 등, 1998; Lynch 와 McConnell, 2002; 김여진 등, 2004). 예를 들어, 하악의 후퇴 (retrognathic mandible)나 급격한 전방경사 (steep anterior guidance)를 보이는 경우에는 ‘전통적인 4 inch’보다 작은 반지름의 교합만곡을 부여하여 교합간섭을 피할 수 있도록 해주고, 반대로 Class Ⅲ 경향을 보이는 경우에는 ‘전통적인 4 inch’보다 큰 반지름의 교합만곡을 부여하여 더 편평한 만곡을 갖도록 구치부 치열을 회복시켜 준다 (Lynch 와 McConnell, 2002). 또한 몬슨 구는 총의치에서 인공치 배열 시 시상 및 측방 조절만곡을 결정할 때에 참고자료로도 이용되어 총의치의 안정을 도모한다 (Bonwill, 1885; 최아영 등, 1998). 이와 같이 자연치열과 인공치열의 교합 재형성에 참고자료로 이용될 수 있는 몬슨 구를 적절하고 효과적으로 활용하기 위해서는 몬슨 구를 정확하게 파악하는 것이 필수적이다.

지금까지 교합만곡에 대한 연구는 많은 학자들에 의해 다양한 방법으로 시도되어 왔으나 대부분 스피만곡에 집중되어 있다 (Osborn, 1987; Osborn과 Francis, 1989; Merz 등, 1991; Ferrario 등, 1992; Osborn, 1993; Baydas 등, 2004; Xu 등, 2004; Craddock 등, 2005; Hayasaki 등, 2005; Cheon 등, 2008). 몬슨 구에 대해서는 1990년대 말 Ferrario 등 (1997)이 3-D digitizer를 이용하여 시상면에서 몬슨 구의 반지름을 측정하면서 비로소 몬슨의 주장에 대한 정량적인 후속연구가 이루어졌다. 이후 Ferrario 등의 후속연구 및 이를 활용한 몇몇의 연구 등이 이루어지고 있으며 (Ferrario 등, 1999; Kagaya 등, 2009), 몬슨 구에 대한 연구는 여전히 부족한 상황이다. 이는 곡선 (curve)과 같은 이차원적 구조가 아니라 구 (sphere)라는 삼차원적 구조 특성 때문에 측정도 어려웠을 것이라 여겨진다.

몬슨 구의 크기는 분석대상이나 분석방법에 따라 보고 된 반지름 값에 차이가 있다 (Ferrario 등, 1997; Ferrario 등, 1999; Kagaya 등, 2009; Nam 등, 2013). Caucasian을 대상으로 3-D digitizer를 이용한 연구들에서는 몬슨 구의 반지름이 ‘전통적인 4 inch’에 상당히 근접하며 성별에 따른 차이는 없다고 보고하였고 (Ferrario 등, 1997; Ferrario 등, 1999), 아시아인을 대상으로 Broadrick occlusal analyzer 및 삼차원 가상모형을 이용한 연구들에서는 약 110.60~110.89 mm (약 4.3 inch)의 반지름을 가지며 성별에 따라 유의한 차이가 있다고 보고하였다 (Kagaya 등, 2009; Nam 등, 2013). 또한, 대부분의 연구에서 몬슨 구의 반지름은 개인에 따른 차이가 큰 경향을 보여 (Ferrario 등, 1997; Ferrario 등, 1999; Kagaya 등, 2009; Nam 등, 2013), 임상적 적용 시 개개인의 치열궁 형태에 맞는 반경을 적용하는 것이 의의가 있다는 주장이 보고되기도 하였다 (Ferrario 등, 1997; 최아영 등, 1998; Farella 등, 2002; Xu 등, 2004).

교합만곡에 영향을 미치는 요인들에 대한 연구는 치열궁의 형태뿐만 아니라 다양한 요인들을 대상으로 그 상관관계가 보고되고 있다. 스피만곡에 영향을 미치는 요인으로는 overbite (Braun 등, 1996; Orthlied, 1997; Baydas 등, 2004), overjet (Baydas 등, 2004), lower arch circumference (Balridge, 1969; Germane 등, 1992; Braun 등, 1996), lower incisor proclination (Balridge, 1969; Alqabandi 등, 1999), arch length (Cheon 등, 2008), craniofacial morphology (Orthlied, 1997; Farella 등, 2002) 등이 있다. 윌슨만곡에 영향을 미치는 요인으로는 상악 윌슨만곡에 영향을 미치는 상악 좌·우측 구치부의 협측 경사도와 하악 윌슨만곡에 영향을 미치는 하악 좌·우측 구치부의 설측 경사도가 있다 (Wilson, 1911). 이에 반해 몬슨 구에 영향을 미치는 요인에 대한 연구는 일본인을 대상으로 몬슨 구의 반지름과 하악 치열궁의 크기, 상하악궁의 수평적·수직적 관계 등의 상관관계를 분석한 Kagaya 등 (2009)의 연구가 유일하며, 하악 치아의 교두 경사각과 몬슨 구의 크기와의 상관관계에 대한 연구는 아직 보고되지 않았다. 따라서 몬슨 구의 측정뿐만 아니라 그에 영향을 미치는 요인들에 대한 분석이 함께 이루어진다면 임상적 적용에 있어서 참고자료로 함께 활용될 수 있을 것이다.

근래 과학 기술의 발전에 힘입어 치과 영역에서도 삼차원 가상모형 (3-D virtual models)이 도입되어 널리 응용되고 있다 (Jemt 와 Lekholm, 2003; Krarup 등, 2005; Lee 등, 2008; Kehl 등, 2011; Nam 등, 2012). 삼차원 가상모형을 이용한 계측 값의 정확성은 계측 자 요인이나 계측 방법 요인이 측정치의 값에 유의한 영향을 주지 않는다는 연구를 통해 이미 검정된 바 있으며 (DeLong 등, 2003; Redlich 등, 2008), 최근에는 삼차원 가상모형을 이용하여 과거 개념적으로만 기술되었던 몬슨 구를 실제 (real)로 재현하는 알고리즘이 개발된 바 있다 (Nam 등, 2013). 따라서 본 연구에서는 최근 개발된 삼차원 가상모형을 이용한 몬슨 구의 측정방법을 이용하여 몬슨 구를 측정하고, 치열궁의 형태와 치아의 교두 경사각을 대상으로 몬슨 구에 영향을 미치는 요인들을 알아보았다.

재료 및 방법

3. 몬슨 구의 구현

본 연구는 몬슨 구의 측정을 위해 Nam 등 (2013)이 최근 발표한 가상 모형을 이용한 몬슨 구의 삼차원적 측정 방법을 따랐다. Nam 등 의 연구에서 사용된 자체 제작 소프트웨어 프로그램 (custom made software program)을 이용하여 좌·우측 견치의 첨두 및 소구치와 대구치의 근·원심 협·설측 교두정을 모두 포함하는 총 26개의 표지점을 얻어내었으며, 제3대구치는 표지점 생성에서 제외하였다 (Fig. 1). 표지점의 추출 단계에서는 사용자가 직접 치축 (long-axis)을 설정하고 관심영역 (region of interest)을 설정해 주면 그 축을 기준으로 관심영역 내에서 최고점을 자동으로 추출하는 알고리즘을 이용하여 표지점 추출의 객관성과 재현성을 높이고자 하였다. 이후 최소 자승법 (least-squares algorithm)에 입각하여, 얻어낸 표지점을 모두 포함하는 근사 구 (fitted sphere)를 생성한 후 각 구의 반지름을 구하였다 (Fig. 2). 본 측정방법에서는 구의 반지름을 얻어내는 전 과정에서 표지점의 추출 이외에는 사용자의 주관이 개입되지 않아 보다 객관적인 결과를 얻을 수 있었으며, 이전의 연구에서 표지점 추출 과정은 높은 재현성을 나타낸 바 있다 (ICC = 0.953 - 0999, p<.001) (Nam 등, 2013).

하악 제2소구치에서 2교두 형과 3교두 형, 하악 제2대구치에서 4교두 형과 5교두 형 등 교두의 개수에 변이를 보이는 모형들이 있었으나 이전의 연구에서 교두의 개수에 따른 몬슨 구의 크기에는 유의한 차이가 없다고 보고한 바 있으므로 (Nam 등, 2013), 본 연구에서는 교두의 수에 따른 변이를 구분하지 않았다.

Figure 1

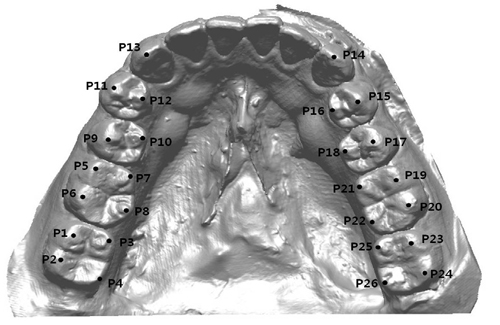
Virtual dental model and reference pointsCusp tips (P13, P14) were identified on canines. Buccal cusp tips (P9, P11, P15 and P17) and lingual cusp tips (P10, P12, P16 and P18) were identified on premolars. Mesio-buccal cusp tips (P1, P5, P19 and P23), disto-buccal cusp tips (P2, P6, P20 and P24), mesio-lingual cusp tips (P3, P7, P21 and P25) and disto-lingual cusp tips (P4, P8, P22 and P26) were identified on molars.

Figure 2

An example of fitted Monson's sphere

Table 1

Measurements related to arch form

Figure 3

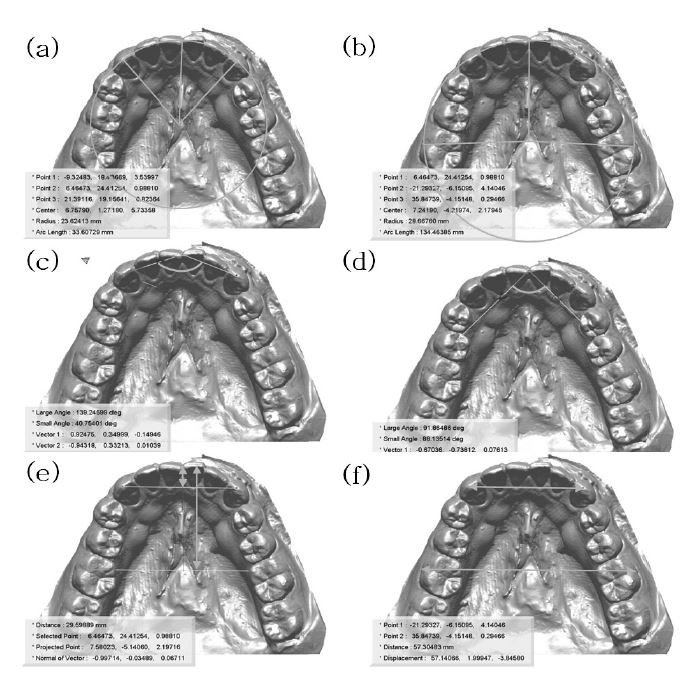
Illustration of measurements related to arch form(a) ICR (incisor to canine radius), (b) IMR (incisor to molar radius), (c) ICA (incisor to canine angle), (d) IMA (incisor to molar angle), (e) IIC (incisor to intercanine line), IIM (incisor to intermolar line), (f) ICW (intercanine width). IMW (intermolar width)

4. 몬슨 구에 영향을 미치는 요인

하악 치열궁의 형태가 몬슨 구에 미치는 영향을 알아보기 위해 이전의 연구에서 상악 치열궁의 형태를 측정하기 위해 사용되었던 항목들을 수정 또는 추가하여 사용하였다 (Park 등, 2007; Lee 등, 2012). 측정에는 RapidForm 2004 (INUS technology INC, Seoul, Korea) 프로그램을 이용하였으며, 측정 항목은 Table 1, Fig 3과 같다.

하악 구치부 치아들의 교두 경사각이 몬슨 구에 미치는 영향을 알아보기 위해 소구치와 대구치부 치아들의 교두 경사각을 측정하였다. 측정을 위해 기준평면으로 좌·우측 견치의 첨두와 제1, 2소구치 및 제1, 2대구치의 교두정을 포함하는 가상근사평면 (virtual fitted plane)을 생성하였다. 이후 좌·우측 소구치와 대구치에서 각 교두정을 연결하는 가상벡터 (virtual vector)들을 생성한 후 가상근사평면과 각 가상벡터들이 이루는 각도로 구치부 치아의 교두 경사각을 측정하였다. 측정에는 마찬가지로 RapidForm 2004 프로그램을 이용하였으며, 측정 항목은 Table 2, Fig 4와 같다.

Table 2

Measurements of cusp angle

Figure 4

Illustration of measurements of cusp angle(a) virtual approximate plane, (b）the vectors connecting the most occlusal points of both buccal / lingual cusp of each tooth, (c), (d) examples of cusp angle measurement

결 과

본 연구에서 측정한 몬슨 구의 평균 반지름은 남자 그룹에서 118.18 ± 26.72 mm, 여자 그룹에서 101.15 ± 19.51 mm 이었으며 남녀 간에는 통계적으로 유의한 차이를 보였다 (p<.001) (Fig. 5). 측정 대상 전체의 평균 반지름은 111.47 ± 25.40 mm (4.39 inch)로 전통적인 4 inch 보다는 다소 큰 값을 나타내었다. 또한 그림에서 보이는 것과 같이 몬슨 구의 반지름은 전체적으로 개인에 따른 차이가 큰 경향을 보였다.

Figure 5

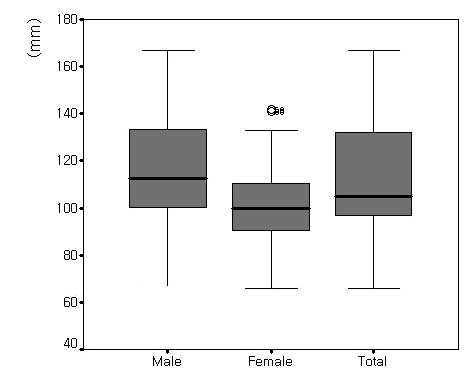
Radius of Monson's sphere in males (43 subjects) and females (28 subjects)Statistical significance were tested by Mann-Whitney test between male and female groups (p<.001).

몬슨 구의 크기에 영향을 미치는 요소들은 하악 치열궁의 형태를 측정한 항목과 하악 구치부 치아들의 교두 경사각을 측정한 항목으로 나누어 측정하였으며 측정 결과는 Table 3과 같다. 치열궁의 형태를 측정한 항목중에서 절치와 좌·우측 견치가 이루는 각도를 측정한 ICA는 몬슨 구의 반지름과 음의 상관관계를 나타내었으며 (p<.05), 치열궁의 길이를 측정한 IIC와 IIM 및 치열궁의 너비를 측정한 ICW와 IMW는 몬슨 구의 반지름과 양의 상관관계를 나타내었다 (p<.05). 특히 견치를 포함하는 항목인 IIC와 ICW에서 그 상관계수가 더 높게 나타났다. 통계적 유의성을 보이는 5개 항목의 상관계수 -0.242 - +0.350의 범위로 높지 않은 경향을 보였다.

Table 3

Descriptive statistics for mandibular arch form and cusp angle and correlations between the radius of Monson's sphere (43 subjects)

구치부 치아의 협·설 교두 경사각은 좌측 제1소구치를 제외한 모든 치아에서 좌·우측이 공통적으로 몬슨 구의 반지름과 음의 상관관계를 나타내었다 (p<.05). 또한 좌·우측 모두 소구치보다는 대구치의 협·설 교두 경사각이 몬슨 구와 높은 상관관계를 보였다. 통계적 유의성을 보이는 11개 항목의 상관계수는 -0.533 - -0.266의 범위로 치열궁의 형태를 측정한 항목들보다 전반적으로 큰 상관계수를 보여, 치열궁의 형태보다는 구치부 개개 치아의 협·설 교두 경사각이 몬슨 구의 크기에 더 큰 영향을 미치는 것을 알 수 있었다.

고 찰

이번 연구에서는 최근 개발된 삼차원 가상모형 상에서의 몬슨 구의 측정방법을 이용하여 몬슨 구를 측정하고, 개인차가 큰 것으로 보고된 바 있는 몬슨 구의 크기에 영향을 미치는 요인들을 알아보고자 하악 치열궁의 형태와 치아의 교두 경사각과의 상관관계를 분석해 보았다.

몬슨 구는 임상적으로 치아의 결손, 정출 및 경사 등에 의해서 생긴 치열의 재형성이나 구강재건술을 시행할 때 교합만곡의 결정기준으로서 널리 응용되며 (Bonwill, 1885; 최아영 등, 1998; Lynch 와 McConnell, 2002; 김여진 등, 2004), 총의치에서 인공치 배열 시 시상 및 측방 조절만곡을 결정할 때에 참고자료로 이용되어 총의치의 안정을 도모한다 (Bonwill, 1885; 최아영 등, 1998). 몬슨에 의해 처음 제창되었던 몬슨의 4 inch 구면설 (Monson, 1920)은 개념적인 서술로만 이어지다가 1990년 대 말이 되어서야 정량적인 값으로 보고가 되었다 (Ferrario, 1997). 몬슨의 발표에서는 연구 대상에 대한 언급이 없었음에도 불구하고 100여 년이 지난 지금까지 임상적으로 다양한 인종과 연령을 대상으로 전통적인 값을 활용하고 있다 (Lynch 와 McConnell, 2002; 김여진 등, 2004). 또한, 여러 연구 결과에서 개인에 따라 구의 반지름이 차이가 보인다고 보고되어 오고 있으나 (Ferrario, 1997; Ferrario, 1999; Kagaya, 2009; Nam, 2013) 개인에 따른 어떠한 요인이 그 반지름 값에 영향을 미치는지에 대해서는 연구가 부족하다. 이와 같이 자연치열과 인공치열의 교합 재형성에 참고자료로 이용될 수 있는 몬슨 구를 임상적으로 효과적인 활용하기 위해서는 몬슨 구를 정확하게 파악할 필요가 있다.

몬슨이 4 inch 구를 정의내린 이후 그 후속연구는 1990년대 말 교합만곡의 분석에 3-D digitizer가 도입되면서 비로소 이루어지기 시작하였다 (Ferrario, 1997). Ferrario 등 (1997) 은 3-D digitizer를 이용하여 얻은 표지점의 삼차원 좌표값을 수학적·통계적 계산을 통해 몬슨 구의 반지름을 측정하였다. 이는 개념적인 서술만으로 정의 내려졌던 몬슨 구의 반지름을 최초의 정량적인 값으로 제시하였다는 점에서 의의가 있지만, 구 중심의 x 축 (치열궁의 좌-우측)을 한 점으로 한정시켜 시상면에서의 몬슨 구의 크기를 측정하였다는 점에서 한계가 있었다. 이후 Kagaya 등 (2009)은 Braodrick occlusal analyzer를 이용하여 분석에 필요한 표지점을 얻은 후 Ferrario 등 (1997, 1999)의 연구방법을 이용하여 일본인을 대상으로 몬슨 구의 반지름을 측정하고 몬슨 구에 영향을 미치는 요인들을 분석한 바 있다.

최근 Nam 등 (2013)은 삼차원 가상모형과 전용의 소프트웨어를 이용하여 몬슨 구를 재현하고 그 반지름을 측정하는 알고리즘을 개발하여, 개념적으로 기술되거나 수학·통계적 계산을 통해 반지름 값을 얻었던 기존의 몬슨 구 연구에서 나아가 그것을 실제 (real)로 재현해 낸 바 있다. 따라서 본 연구에서는 Nam 등 (2013)이 제시한 가상모형을 이용한 몬슨 구의 삼차원적 측정방법을 따라 몬슨 구를 재현하고 그 반지름을 측정하였다.

본 연구에서 얻은 몬슨 구의 반지름은 111.47 ± 25.40 mm (약 4.39 inch)로 기존 몬슨의 연구 (classical 4 inch) 보다는 큰 값을 보였다 (Fig 5). 또한 남자 그룹에서는 평균 반지름이 118.18 ± 26.72 mm인 반면 여자 그룹에서는 평균 반지름이 101.15 ± 19.51 mm로, 남자 그룹이 여자 그룹보다 약 17.03 mm 큰 것을 확인할 수 있었다 (p<.001). 이는 본 연구에서 측정방법을 인용한 Nam 등 (2013)의 연구 결과와 일치하는 경향을 나타내었다. 그러나 몬슨 구에 대한 최초의 정량적 측정 결과를 제시한 Ferrario 등 (1997, 1999)은 Caucasian을 대상으로 한 두 번의 연구에서, 몬슨 구의 평균 반지름은 101.03 - 102.13 mm (약 3.99 - 4.02 inch)로 전통적인 4 inch에 상당히 근접하며 성별에 따른 유의한 차이는 없다고 보고하였다. Kagaya 등 (2009)은 일본인을 대상으로 몬슨 구의 크기를 측정 한 결과, 평균 반지름은 110.60 mm (약 4.35 inch)로 기존 몬슨의 연구 값보다 컸으며 여자 그룹이 남자 그룹에 비해 반지름이 작고 구의 중심이 더 하방에 위치한다는 결과를 보고한 바 있다. 뿐만 아니라 Ferrario 등의 연구 결과와의 차이를 언급하여 몬슨 구의 크기에 인종 간 차이가 있음을 제시하기도 하였다. 그러나 본 연구와 Ferrario 등 및 Kagaya 등의 각 연구들은 측정대상 뿐만 아니라 측정방법에도 차이가 있었으므로 인종에 따른 몬슨 구의 크기에 차이가 있다는 결론을 얻기 위해서는 추가적인 연구가 필요하다.

지금까지 이루어진 대부분의 몬슨 구에 대한 연구들은 공통적으로 구의 반지름이 개인에 따라 다양하다는 경향을 보였으며 본 연구에서도 그 결과를 확인할 수 있었다. 따라서 본 연구에서는 몬슨 구의 반지름에 어떠한 요인들이 영향을 미치는지를 알아보고자 하악 치열궁의 형태와 하악 구치부 치아들의 교두 경사각을 측정하고 그 상관관계를 구하였다 (Table 3).

하악 치열궁의 형태는 치열궁의 반지름과 각도, 길이, 너비 등을 견치부위와 제1대구치 부위에서 각각 측정하였다. 중절치에서 견치까지의 길이를 측정한 IIC와 중절치에서 제1소구치까지의 길이를 측정한 IIM (Fig. 3(e) ), 좌·우측 견치간의 거리를 측정한 ICW와 좌·우측 제1대구치간의 거리를 측정한 IIM (Fig. 3(f) ) 등 치열궁의 길이와 너비를 측정한 4개의 항목들은 모두 몬슨 구의 반지름과 양의 상관관계를 나타내었다. 특히 이들 항목은 대구치부 보다는 견치부에서 공통적으로 높은 상관관계를 보여 구치부 보다는 견치부 치아의 위치나 형태가 몬슨 구에 더 큰 영향을 미친다는 것을 알 수 있었다. 다만 상관계수가 0.242 - 0.350으로 크지 않아 치열궁의 형태와 몬슨 구의 크기와의 상관관계에 대해 큰 의미를 부여하기는 어려웠다. 치열궁의 형태와 몬슨 구와의 상관관계에 대한 선행연구로는 Kagaya 등 (2009)의 연구가 유일한데, 수평피개 (overjet), 수직피개 (overbite), 하악 치열궁의 너비 및 길이 가운데 수직피개만이 몬슨 구와 유의한 상관관계를 가진다고 보고한 바 있다 (p<.05).

하악 구치부 치아들의 협·설 교두 경사각은 가상근사평면 (virtual fitted plane)과 구치부 치아들의 협설 교두들을 연결한 가상벡터 (virtual vector)가 이루는 각도로 측정하였다. 우측 제1소구치를 제외한 모든 구치부 치아에서 좌·우측이 공통적으로 몬슨 구의 반지름과 음의 상관관계를 나타내 구치부 치아의 교두 경사각이 완만해 질수록 몬슨 구는 커진다는 것을 알 수 있었다. 특히 소구치부에서의 상관계수는 -0.340 - -0.266의 범위를 나타낸 반면 대구치부에서의 상관계수는 -0.533 - -0.276의 범위를 나타내어 소구치보다는 대구치의 교두 경사각이 몬슨 구의 크기에 더 큰 영향을 미치는 것으로 나타났다. 이러한 경향은 몬슨 구의 정의에 내포되어 있는 윌슨만곡에 영향을 미치는 요인에 대한 이전의 연구에서도 찾아볼 수 있는데, 하악의 윌슨만곡은 하악 좌·우측 대구치 치아의 설측 교두 경사각에 영향을 받는다는 연구 결과가 보고된 바 있어 (Wilson, 1911; The glossary of prosthodontic terms, 2005) 본 연구 결과를 뒷받침해주고 있다. 몬슨 구에 영향을 미치는 요인으로 하악 치아의 교두 경사도와의 상관관계에 대한 연구는 지금까지 보고된 바가 없어 이번 연구를 토대로 교두 경사도가 교합만곡에 미치는 영향에 대한 다양한 연구가 이루어질 수 있을 것으로 기대된다. 뿐만 아니라, 이번 연구에서 몬슨 구에 유의하게 영향을 미치는 것으로 나타난 11개의 요인들은 전반적으로 치열궁의 형태보다는 구치부의 교두 경사각을 측정한 항목들에서 높은 상관계수를 나타내어 하악 치열궁의 형태보다는 하악 구치부 치아들의 협·설 경사도가 몬슨 구의 크기에 더 큰 영향을 미친다는 것을 알 수 있었다.

이번 연구 결과를 토대로, 임상적으로 구치부 치열의 재형성과정에서 광범위한 교합파괴가 동반된 경우 잔존 대구치부 치아의 협·설 교두 경사각이나 구강 내 생존률이 높은 견치부의 악궁의 형태 등을 참고하여 몬슨 구의 크기를 조절한다면 보다 적절한 교합만곡을 부여해 줄 수 있을 것이다. 즉, 잔존 대구치부 치아의 협·설 교두 경사가 완만하거나 견치부 악궁의 길이가 긴 경우 및 견치간 거리가 넓은 경우에는 평균적인 몬슨 구보다 큰 반지름을 적용하여 교합의 안정성을 부여해 줄 수 있다 (Lynch 와 McConnell, 2002). 또한 총의치에서 인공치의 배열 시에 치열궁의 형태를 고려한 몬슨 구를 부여해 준다면 보다 안정적인 교합을 부여해 줄 수 있을 것이다 (Bonwill, 1885; 최아영 등, 1998).

본 연구에서는 몬슨 구의 측정을 위해 표지점을 얻어내야 하는 교합면 부위에 보철물이 없는 건전한 자연치를 가지고 있는 성인의 모형을 확보하는데 어려움이 있었다. 이번 연구 결과를 바탕으로 향후 연구에서는 더 많은 모형을 대상으로 한 분석이 필요하다. 또한 교합은 치아, 악관절, 근육, 신경 등의 상호작용에 의해 이루어지는 삼차원적 운동이므로, 악궁 내 요인뿐만 아니라 상·하악 악관관계나 두개 안면부의 골 및 근육 등 더 다양한 요인들도 함께 고려한다면 더 의미있는 결과를 얻을 수 있을 것이다.

결 론

본 연구에서는 삼차원 가상분석 상에서의 분석 방법을 이용하여 몬슨 구를 측정하고 그에 영향을 미치는 요소로 하악 치열궁의 형태와 하악 구치부 치아의 교두 경사각과의 상관관계에 대해 알아보았다. 한국인을 대상으로 얻은 몬슨 구의 반지름은 111.47 mm (약 4.39 inch)로 전통적인 4 inch 보다는 다소 큰 경향을 보였으며, 하악 치열궁의 형태보다는 하악 구치부 치아들의 교두 경사각이 몬슨 구에 더 큰 영향을 미친다는 것을 알 수 있었다. 특히, 몬슨 구에 가장 큰 영향을 미치는 항목은 하악 좌·우측 대구치의 협·설측 교두 경사각과 하악 견치부 악궁의 길이 및 견치간 거리 등으로 나타났다. 임상적으로 구치부 치열의 재형성이나 인공치 배열 시에 몬슨 구의 반지름을 적용하는 경우, 전통적인 4 inch 보다는 큰 값을 부여해 주며 동시에 하악 대구치부의 교두 경사각이나 견치부 악궁의 형태 등의 개인차를 고려하여 그 값을 조절해 준다면 보다 의미있게 몬슨 구를 적용할 수 있을 것이라 생각된다.

Acknowledgments

본 연구는 보건복지부 보건의료기술연구개발사업의 지원에 의하여 이루어진 것임. A(091074).

References

• AK Alqabandi, Sadowsky, EA Begole, A comparison of the effects of rectangular and round arch wires in leveling the curve of Spee, Am J Orthod Dentofacial Orthop, (1999), 116, p522-529. [https://doi.org/10.1016/S0889-5406(99)70183-6]
• DW Balridge, Leveling the curve of Spee: its effect on the mandibular arch length, J Pract Orthod, (1969), 3, p26-41.
• B Baydas, I Yavuz, N Atasaral, I Ceylan, IM Dagsuyu, Investigation of the changes in the positions of upper and lower incisors, overjet, overbite, and irregularity index in subjects with different depths of curve of Spee, Angle Orthod, (2004), 74, p349-355.
• WGA Bonwill, The geometrical and mechanical laws of the articulation of the human teeth: the anatomical articulator, In: F L, editor. The American system of dentistry. Philadelphia: Lea Brothers, (1885), p486-498.
• S Braun, WP Hnat, BE Johnson, The curve of Spee revisited, Am J Orthod Dentofacial Orthop, (1996), 110, p206-210. [https://doi.org/10.1016/S0889-5406(96)70110-5]
• SH Cheon, YH Park, KS Paik, SJ Ahn, K Hayashi, WJ Yi, SP Lee, Relationship between the curve of Spee and dentofacial morphology evaluated with a 3-dimensional reconstruction method in Korean adults, Am J Orthod Dentofacial Orthop, (2008), 133(640), pe647-e614. [https://doi.org/10.1016/j.ajodo.2007.11.020]
• HL Craddock, CD Lynch, P Franklin, CC Youngson, M Manogue, A study of the proximity of the Broadrick ideal occlusal curve to the existing occlusal curve in dentate patients, J Oral Rehabil, (2005), 32, p895-900. [https://doi.org/10.1111/j.1365-2842.2005.01520.x]
• R DeLong, M Heinzen, JS Hodges, CC Ko, WH Douglas, Accuracy of a system for creating 3D computer models of dental arches, J Dent Res, (2003), 82, p438-442. [https://doi.org/10.1177/154405910308200607]
• M Farella, A Michelotti, R Martina, The curve of Spee and craniofaical morphology: a multiple regression analysis, Eur J Oral Sci, (2002), 110, p277-281.
• VF Ferrario, C Sforza, A Miani Jr, Statistical evaluation of Monson's sphere in healthy permanent dentitions in man, Arch Oral Biol, (1997), 42, p365-369. [https://doi.org/10.1016/S0003-9969(97)00021-6]
• VF Ferrario, C Sforza, A Miani Jr, A Colombo, G Tartaglia, Mathematical definition of the curve of Spee in permanent healthy dentitions in man, Arch Oral Biol, (1992), 37, p691-694. [https://doi.org/10.1016/0003-9969(92)90073-H]
• VF Ferrario, C Sforza, CE Poggio, G Serrao, A Colombo, Three-dimensional dental arch curvature in human adolescents and adults, Am J Orthod Dentofacial Orthop, (1999), 115, p401-405. [https://doi.org/10.1016/S0889-5406(99)70259-3]
• N Germane, JA Staggers, L Rubenstein, JT Revere, Arch length considerations due to the curve of Spee: a mathematical model, Am J Orthod Dentofacial Orthop, (1992), 102, p251-255. [https://doi.org/10.1016/S0889-5406(05)81060-1]
• H Hayasaki, RP Martins, LG Gandini, I Saitoh, K Nonaka, A new way of analyzing occlusion 3 dimensionally, Am J Orthod Dentofacial Orthop, (2005), 128, p128-132. [https://doi.org/10.1016/j.ajodo.2004.07.039]
• T Jemt, U Lekholm, Measurements of buccal tissue volumes at single-implant restorations after local bone grafting in maxillas: a 3-year clinical prospective study case series, Clin Impl Dent Relat Res, (2003), 5, p63-70. [https://doi.org/10.1111/j.1708-8208.2003.tb00185.x]
• K Kagaya, I Minami, T Nakamura, M Sato, T Ueno, Y Igarashi, Three-dimensional analysis of occlusal curvature in healthy Japanese young adults, J Oral Rehabil, (2009), 36, p257-263. [https://doi.org/10.1111/j.1365-2842.2008.01930.x]
• M Kehl, K Swierkot, R Mengel, Three-dimensional measurement of bone loss at implants in patients with periodontal disease, J Periodontol, (2011), 82, p689-699. [https://doi.org/10.1902/jop.2010.100318]
• S Krarup, TA Darvann, P Larsen, JL Marsh, S Kreiborg, Three-dimensional analysis of mandibular growth and tooth eruption, J Anat, (2005), 207, p669-682. [https://doi.org/10.1111/j.1469-7580.2005.00479.x]
• SP Lee, R Delong, JS Hodges, K Hayashi, JB Lee, Predicting first molar width using virtual models of dental arches, Clin Anat, (2008), 21, p27-32. [https://doi.org/10.1002/ca.20580]
• SP Lee, SJ Lee, K Hayashi, YS Park, A three-dimensional analysis of the perceived proportions of maxillary anterior teeth, Acta Odontol Scand, (2012), 70, p432-440. [https://doi.org/10.3109/00016357.2011.600716]
• CD Lynch, RJ McConnell, Prosthodontic management of the curve of Spee: use of the Broadrick flag, J Prosthet Dent, (2002), 87, p593-597. [https://doi.org/10.1067/mpr.2002.125178]
• ML Merz, RJ Isaacson, N Germane, Rubenstein Rubenstein, Tooth diameters and arch perimeters in a black and a white population, Am J Orthod Dentofacial Orthop, (1991), 100, p53-58. [https://doi.org/10.1016/0889-5406(91)70049-3]
• GS Monson, Occlusion as applied to crown and bridgework, J Nat Dent Assoc, (1920), 7, p399-413.
• SE Nam, YH Kim, YS Park, SH Baek, K Hayashi, KN Kim, SP Lee, Three-dimensional dental model constructed from an average dental form, Am J Orthod Dentofacial Orthop, (2012), 141, p213-218. [https://doi.org/10.1016/j.ajodo.2011.06.038]
• SE Nam, YS Park, HR Ryu, YS Lim, SP Lee, Comparisons of tooth wear of the first molar in Korean and Japanese using new quantitative mea measurement parameters, J Korean Res Soc Dent Materials, (2012), 39, p241-250.
• SE Nam, YS Park, W Lee, Ahn Ahn, SP Lee, Making three-dimensional Monson's sphere using virtual dental models, J Dent, (2013), 41, p336-344. [https://doi.org/10.1016/j.jdent.2013.01.003]
• JD Orthlied, The curve of Spee: understanding the sagittal organization of mandibular teeth, Cranio, (1997), 15, p333-340.
• JW Osborn, Relationship between the mandibular condyle and the occlusal plane during hominid evolution: some of its effects on jaw mechanics, Am J Phys Anthropol, (1987), 73, p193-207. [https://doi.org/10.1002/ajpa.1330730206]
• JW Osborn, LJ Francis, The position of the dentition in the mandible and its possible relation to orthodontic abnormalities, Am J Orthod Dentofacial Orthop, (1989), 96, p327-332. [https://doi.org/10.1016/0889-5406(89)90352-1]
• JW Osborn, Orientation of the masseter muscle and the curve of Spee in relation to crushing forces on the molar teeth of primates, Am J Phys Anthropol, (1993), 92, p99-106. [https://doi.org/10.1002/ajpa.1330920108]
• YS Park, SP Lee, KS Paik, The threedimensional relationship on a virtual model between the maxillary anterior teeth and incisive papilla, J Prosthet Dent, (2007), 98, p312-318.
• M Redlich, T Weinstock, Y Abed, R Schneor, Y Holdstein, A Fischer, A new system for scanning, measuring and analyzing dental casts based on a 3D holographic sensor, Orthod Craniofac Res, (2008), 11, p90-95. [https://doi.org/10.1111/j.1601-6343.2007.00417.x]
• FG Spee, Die Verschiebungsbahn des Unterkiefers am Schädel, Archives fur Anatomie und Physiologie, (1890), 16, p285-294.
• GH Wilson, A manual of dental prosthetics, Philadelphia: Lea & Febiger, (1991), p22-37.
• H Xu, T Suzuki, M Muronoi, K Ooya, An evaluation of the curve of Spee in the maxilla and mandible of human permanent healthy dentitions, J Prosthet Dent, (2004), 92, p536-539. [https://doi.org/10.1016/j.prosdent.2004.08.023]
• The glossary of prosthodontic terms, J Prosthet Dent, (2005), 294, p10-92.